Problem description:

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.

Example 1:

1
2
3
4
5
6
7
8
9
10
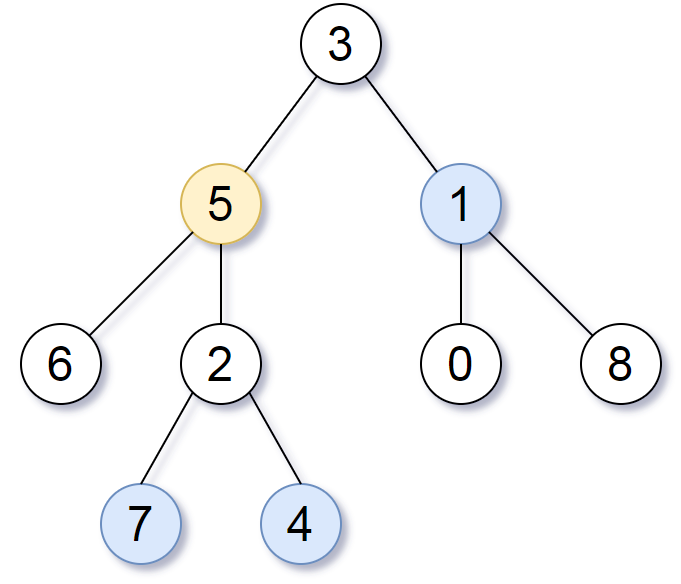
Input:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2

Output:[7,4,1]

Explanation:
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.

Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

https://s3-lc-upload.s3.amazonaws.com/uploads/2018/06/28/sketch0.png

Note:

  1. The given tree is non-empty.
  2. Each node in the tree has unique values 0 <= node.val <= 500.
  3. The target node is a node in the tree.
  4. 0 <= K <= 1000.

Solution:

We don’t know the relation from target to node on top of it or on the other side of tree. So we construct a new graph from tree.

  1. DFS, Build graph that each node knows its parent and child
  2. BFS, find level by level
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def distanceK(self, root: TreeNode, target: TreeNode, K: int) -> List[int]:
        # build graph from tree
        graph = defaultdict(list)
        def buildGraph(parent, child):     
            if not child:
                return 
            if parent: graph[child].append(parent)
            if child.left: 
                graph[child].append(child.left)
                buildGraph(child, child.left)
            if child.right: 
                graph[child].append(child.right)
                buildGraph(child, child.right)
        
        buildGraph(None, root)
        
        res, queue, visited = [], deque(), set()
        queue.append((target, 0))
        while queue:
            # BFS, find distant K nodes
            node, dis = queue.popleft()
            
            # base case, if this node visited, skip
            if node in visited:
                continue
            visited.add(node)
            if dis == K:
                res.append(node.val)   
            elif dis < K: # keep finding distance longer nodes
                for neighbor in graph[node]:
                    queue.append((neighbor, dis+1))
        return res

time complexity: $O()$
space complexity: $O()$
reference:
related problem: