Problem description:

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

  • lefti is the x coordinate of the left edge of the ith building.
  • righti is the x coordinate of the right edge of the ith building.
  • heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

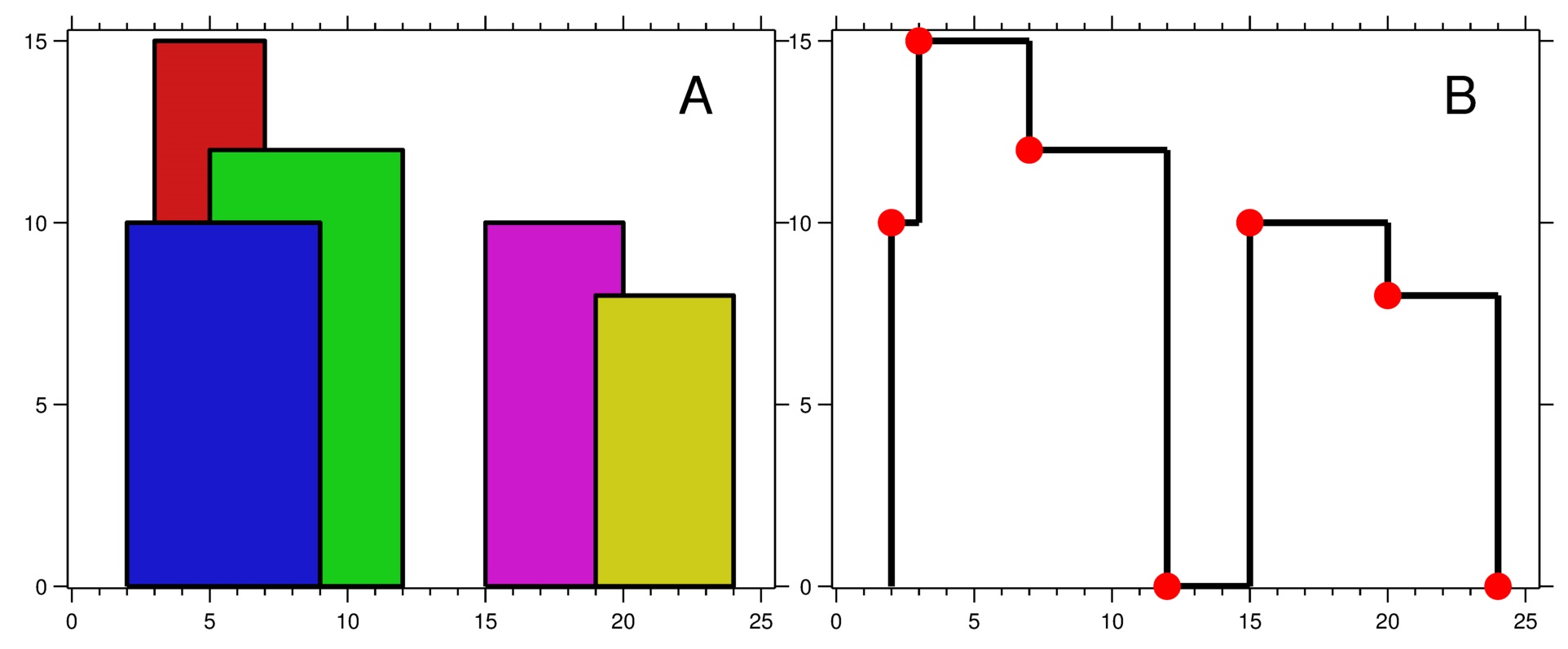
https://assets.leetcode.com/uploads/2020/12/01/merged.jpg

1
2
3
4
5
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

1
2
Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints:

  • 1 <= buildings.length <= 104
  • 0 <= lefti < righti <= 231 - 1
  • 1 <= heighti <= 231 - 1
  • buildings is sorted by lefti in non-decreasing order.

Solution:

for each critical point c c.y gets the height of the tallest rectangle over c

This is no longer obviously O(n^2). If we can somehow calculate the height of the tallest rectangle over c in faster than O(n) time, we have beaten our O(n^2) algorithm. Fortunately, we know about a data structure which can keep track of an active set of integer-keyed objects and return the highest one in O(log⁡n) time: a (max) heap.

Our final solution, then, in O(nlog⁡n) time, is as follows. First, sort the critical points. Then scan across the critical points from left to right. When we encounter the left edge of a rectangle, we add that rectangle to the heap with its height as the key. When we encounter the right edge of a rectangle, we remove that rectangle from the heap. (This requires keeping external pointers into the heap.) Finally, any time we encounter a critical point, after updating the heap we set the height of that critical point to the value peeked from the top of the heap.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        events = []
        for L, R, H in buildings:
            events.append((L, -H, R)) 
            # start event, using min heap so append -H
            # need that -H in the list, not just for the heap. Because, when you sort events, you want to make sure for given x an event with max H is processed first. ex: height 14 vs 15, after negative, -15 event would come before -14 event
            events.append((R, 0, 0))
        events.sort()
        
        res = [(0, 0)]
        heap = [(0, float('inf'))]
        
        for pos, negH, R in events:
            # processing events
            # 1. cleanout old events by pop out those right ends before new event
            # 2. push the new events to the queue
            # 3. check if new largest height affect result skyline
            
            # pop out building which is end
            while heap[0][1] <= pos:
                heapq.heappop(heap)
            
            # if it is a start of building, push it into heap as current building
            if negH != 0:
                heapq.heappush(heap, (negH, R))
            
            # if change in height with previous key point, append to result
            if res[-1][1] != -heap[0][0]:
                res.append([pos, -heap[0][0]])
        return res[1:]

time complexity: $O(nlogn)$
space complexity: $O(n)$
reference:
https://briangordon.github.io/2014/08/the-skyline-problem.html
related problem: