Problem description:

Storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.

The game is represented by a grid of size m x n, where each element is a wall, floor, or a box.

Your task is move the box 'B' to the target position 'T' under the following rules:

  • Player is represented by character 'S' and can move up, down, left, right in the grid if it is a floor (empy cell).
  • Floor is represented by character '.' that means free cell to walk.
  • Wall is represented by character '#' that means obstacle (impossible to walk there).
  • There is only one box 'B' and one target cell 'T' in the grid.
  • The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
  • The player cannot walk through the box.

Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.

Example 1:

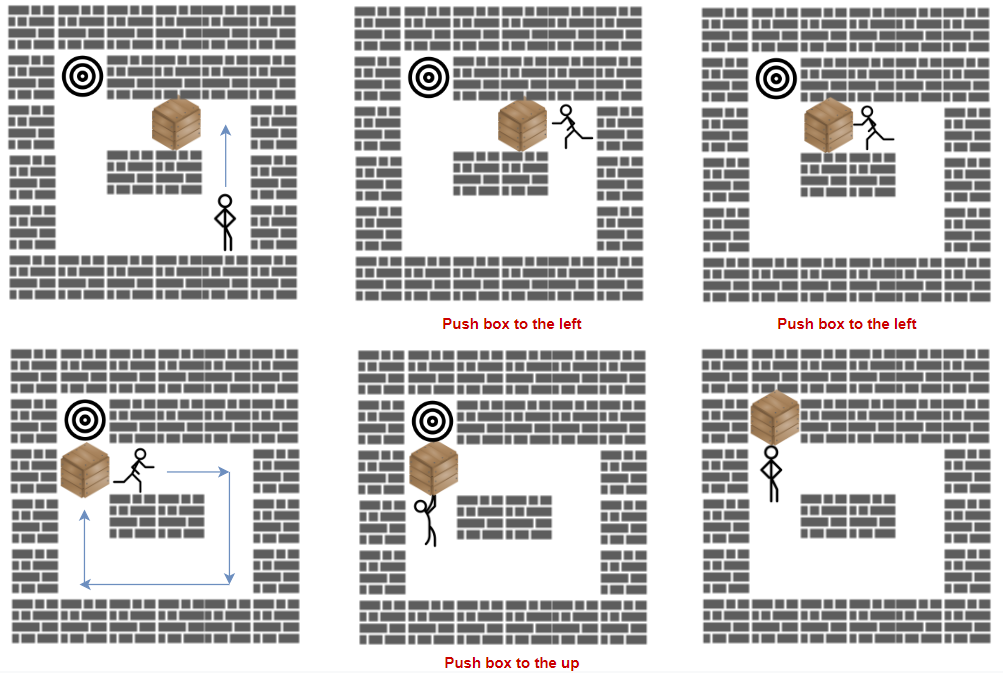
https://assets.leetcode.com/uploads/2019/11/06/sample_1_1620.png

1
2
3
4
5
6
7
8
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation:We return only the number of times the box is pushed.

Solution:

Dijkstra, a node is (person, box) tuple, weight is the number of moves

  1. First find all the positions and set of free spots, note everyplace is free spot except wall #
  2. Do BFS with heap, moves is the weight of edge
  3. For every direction to move person, there’re two cases
    1. New position is not box located:
      Node (newPerson location, box) not yet visited
      Node (newPerson location) is in free spot sets
      note that we don’t have to increase move
    2. New position is box located:
      Node (newPerson location, newBox location) not yet visited
      Node (newBox location) is in free spot sets
      need to increase move because we move the box
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution:
    def minPushBox(self, grid: List[List[str]]) -> int:
        '''
        dijkstra, get all nodes, start with lowest weight edge
        expand the node by checking if could move person or box
        '''
        m, n = len(grid), len(grid[0])
        free = set()
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 'S':
                    person = (i, j)
                elif grid[i][j] == 'B':
                    box = (i, j)
                elif grid[i][j] == 'T':
                    target = (i, j)
                if grid[i][j] != '#': # note every place except wall is free 
                    free.add((i,j))
        # print(box, person, target)
        def valid(i, j):
            return 0 <= i < m and 0 <= j < n and grid[i][j] != '#'
        
        # Dijkstra, start with min weight weight edges
        # heap = [(0, person[0], person[1], box[0], box[1])]
        visited = set()
        
        heap = [(0, person[0], person[1], box[0], box[1])]
        
        while heap:
            moves, px, py, bx, by = heappop(heap)
            print(moves, px, py, bx, by)
            # dx, dy = 
            if (bx, by) == target:
                return moves
            if (px, py, bx, by) in visited:
                continue
            
            visited.add((px, py, bx, by))
            for dx, dy in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                # able to move player, note it doesn't make move+1
                # able to move box
                
                nx, ny = px+dx, py+dy
                if (nx, ny, bx, by) not in visited and (nx, ny) in free and (nx, ny) != (bx, by):
                    heappush(heap, (moves, nx, ny, bx, by))
                elif (nx, ny) == (bx, by) and (nx, ny, bx+dx, by+dy) not in visited and (bx+dx, by+dy) in free:
                    # print((nx, ny, bx, by))
                    heappush(heap, (moves+1, nx, ny, bx+dx, by+dy))
        return -1

Two BFS: one to find if person could move to new position to push box; the other one to find box could move to target position

  1. Lets think that we have no person and we have to find the minimum path between box and the target. Easy right? Simple BFS.
  2. If you know how to solve the first part, what I actually do is modified first part with few constraints.
    • I just check whether the box can be shifted to the new position(up, down, left, right)
    • For it to be shifted to the new position the person has to be in a corresponding position right?
    • So we check if the person can travel from his old position to his corresponding new position(using another BFS).
    • If the person can travel to his new position than the box can be shifted, otherwise the box cannot be shifted.
  3. We keep repeating step 2 until we reach the target or it is not possible to move the box anymore.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution:
    def minPushBox(self, grid: List[List[str]]) -> int:
        # find person, target, box
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 'S':
                    person = (i,j)
                if grid[i][j] == 'T':
                    target = (i,j)
                if grid[i][j] == 'B':
                    box = (i,j)
        # 
        def valid(i, j):
            return 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] != '#'
        
        def check(cur, dest, box):
            q = deque([cur])
            v = set()
            while q:
                pos = q.popleft()
                if pos == dest:
                    return True
                newPos = [(pos[0]+1, pos[1]), (pos[0]-1, pos[1]), (pos[0], pos[1]+1), (pos[0], pos[1]-1)]
                for x, y in newPos:
                    if valid(x, y) and (x,y) not in v and (x,y) != box:
                        v.add((x,y))
                        q.append((x,y))
            return False
        
        # since we need to know the distance to walk, tuple contains dis
        q = deque([(0, box, person)])
        visited = {box+person}
        
        while q:
            dis, box, person = q.popleft()
            if box == target:
                return dis
            
            b_coord = [(box[0]+1, box[1]),(box[0]-1, box[1]),(box[0], box[1]+1),(box[0], box[1]-1)]
            p_coord = [(box[0]-1, box[1]),(box[0]+1, box[1]),(box[0], box[1]-1),(box[0], box[1]+1)]
            for newBox, newPerson in zip(b_coord, p_coord):
                if valid(*newBox) and newBox+box not in visited:
                    if valid(*newPerson) and check(person, newPerson, box):
                        visited.add(newBox+box)
                        q.append((dis+1, newBox, box))
        return -1

time complexity: $O()$
space complexity: $O()$
reference:
related problem: