Problem description:

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.

Example 1:

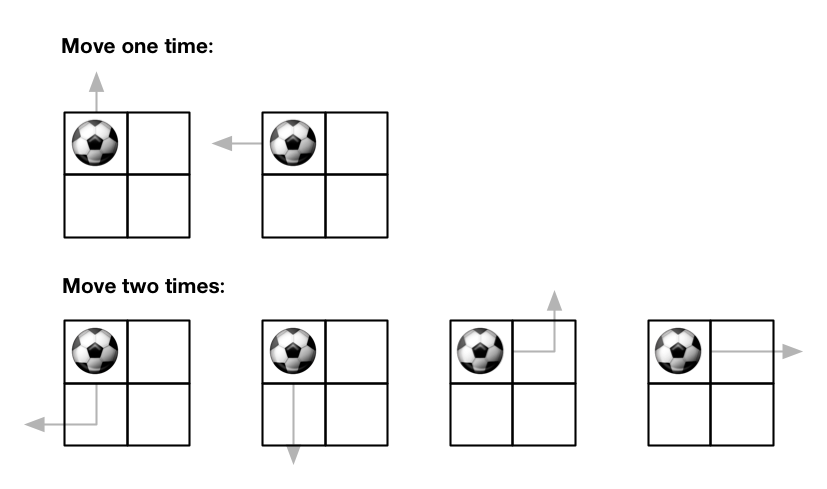
https://assets.leetcode.com/uploads/2021/04/28/out_of_boundary_paths_1.png

1
2
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6

Example 2:

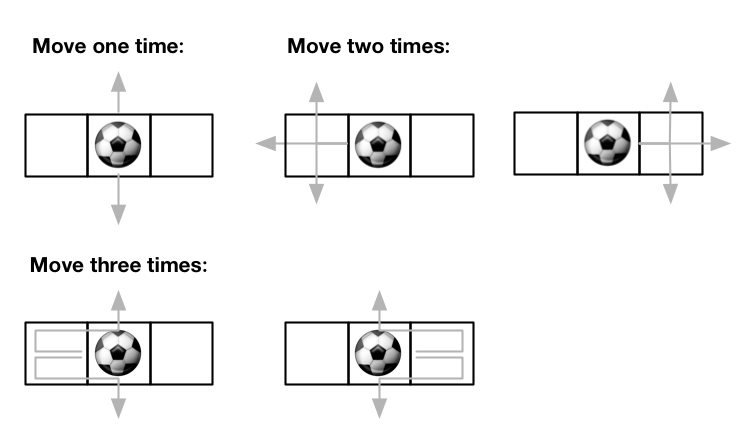
https://assets.leetcode.com/uploads/2021/04/28/out_of_boundary_paths_2.png

1
2
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12

Constraints:

  • 1 <= m, n <= 50
  • 0 <= maxMove <= 50
  • 0 <= startRow < m
  • 0 <= startColumn < n

Solution:

Naive solution: check 4 directions

Improve: memorization to reduce duplicate calculation when we reach to the same spot with same moves left.

First idea we could come up with a naive solution to calculate we have moves left when we walk the array like the following. 

1
2
3
4
if maxMove < 0:
	return 0
if out of boundary:
	return 1

When we reach to a new position, we need to check 4 directions

1
2
3
4
5
6
a = solve(i-1, j, move-1)
b = solve(i+1, j, move-1)
c = solve(i, j-1, move-1)
d = solve(i, j+1, move-1)

res = a+b+c+d

However, the above naive solution takes O(4^n)

We could add a dp array to keep the calculation that we’ve already done. The idea is that when we reach to a specific position with specific moves left, the amount of out of boundary ways are fixed.

Situations like [ i = 1, j = 1, max_moves = 1] will be calculated many times, e.g.:

  • max_moves = 2 and coming left from (1, 2)
  • going right from (1, 0)
  • coming down from (0, 1)
  • going up from (2, 1)

So ,why to solve 4 times for the same [ i = 1, j = 1, max_moves = 1]. Better to memoize/store the computed result in some data structure and return the result directly next time without actually computing [ i = 1, j = 1, max_moves = 1] again.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
        # idea is to create dp array to memorize the state when we get to each (i,j) and x moves
        dp = [[[-1]*(maxMove+1) for _ in range(n+1)] for _ in range(m+1)]
        
        def solve(i, j, move):
            # a recursive function to update dp 
            if move < 0: 
                return 0
            if i < 0 or j < 0 or i >= m or j >= n:
                return 1 # find one path that could be out of boundary
            
            if dp[i][j][move] != -1:
                return dp[i][j][move]
            
            a = solve(i-1, j, move-1)
            b = solve(i+1, j, move-1)
            c = solve(i, j-1, move-1)
            d = solve(i, j+1, move-1)
            
            dp[i][j][move] = a+b+c+d
            return dp[i][j][move]
        
        return solve(startRow, startColumn, maxMove) % (10**9 +7)

time complexity: $O(mnmoves)$, $O(n^3)
space complexity: $O(mnmoves)$
reference:
related problem: