Problem description:

Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.

Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.

Example 1:

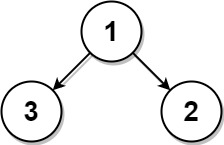
https://assets.leetcode.com/uploads/2021/06/13/closest1-tree.jpg

1
2
3
Input: root = [1,3,2], k = 1
Output: 2
Explanation: Either 2 or 3 is the nearest leaf node to the target of 1.

Example 2:

https://assets.leetcode.com/uploads/2021/06/13/closest2-tree.jpg

1
2
3
Input: root = [1], k = 1
Output: 1
Explanation: The nearest leaf node is the root node itself.

Example 3:

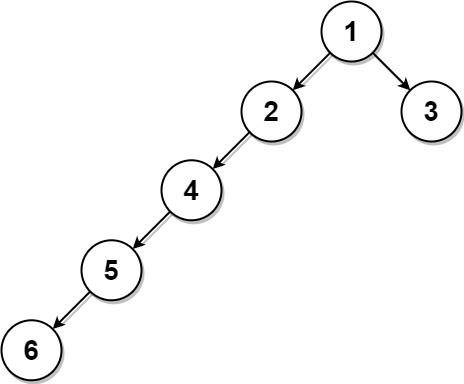
https://assets.leetcode.com/uploads/2021/06/13/closest3-tree.jpg

1
2
3
Input: root = [1,2,3,4,null,null,null,5,null,6], k = 2
Output: 3
Explanation: The leaf node with value 3 (and not the leaf node with value 6) is nearest to the node with value 2.

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • 1 <= Node.val <= 1000
  • All the values of the tree are unique.
  • There exist some node in the tree where Node.val == k.

Solution:

To find the leave in another half of tree, we need to build graph to find every node’s neighbor.

In the meantime, keep all the leaves in a set.

Do BFS to see which neighbor is the first leaf

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findClosestLeaf(self, root: TreeNode, k: int) -> int:
        # build neighbor graph to find the nearest leaf by bfs
        graph, leaves = defaultdict(list), set()
        # Graph construction
        def traverse(node):
            if not node:
                return
            if not node.left and not node.right:
                leaves.add(node.val)
                return
            if node.left:
                graph[node.val].append(node.left.val)
                graph[node.left.val].append(node.val)
                traverse(node.left)
            if node.right:
                graph[node.val].append(node.right.val)
                graph[node.right.val].append(node.val)
                traverse(node.right)
        traverse(root)
        # Graph traversal - BFS
        queue, visited = [k], set()
        while len(queue):
            level = []
            for node in queue:
                if node not in visited:
                    if node in leaves:
                        return node
                    level += graph[node]
                    visited.add(node)
            queue = level

time complexity: $O(n)$
space complexity: $O(n)$
reference:
related problem: