Problem description:

The boundary of a binary tree is the concatenation of the root, the left boundary, the leaves ordered from left-to-right, and the reverse order of the right boundary.

The left boundary is the set of nodes defined by the following:

  • The root node’s left child is in the left boundary. If the root does not have a left child, then the left boundary is empty.
  • If a node in the left boundary and has a left child, then the left child is in the left boundary.
  • If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary.
  • The leftmost leaf is not in the left boundary.

The right boundary is similar to the left boundary, except it is the right side of the root’s right subtree. Again, the leaf is not part of the right boundary, and the right boundary is empty if the root does not have a right child.

The leaves are nodes that do not have any children. For this problem, the root is not a leaf.

Given the root of a binary tree, return the values of its boundary.

Example 1:

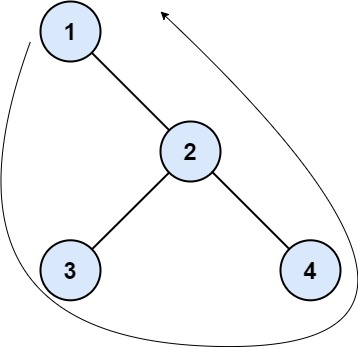
https://assets.leetcode.com/uploads/2020/11/11/boundary1.jpg

1
2
3
4
5
6
7
8
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
Explanation:
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
  4 is a leaf, so the right boundary is [2].
- The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].

Example 2:

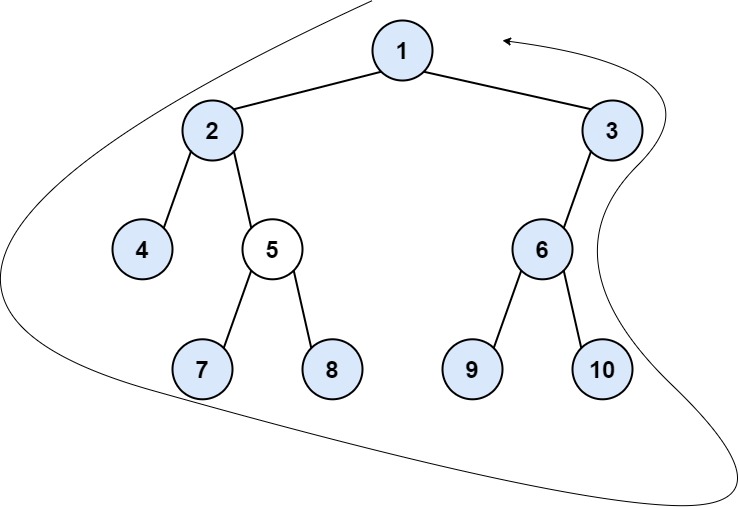
https://assets.leetcode.com/uploads/2020/11/11/boundary2.jpg

1
2
3
4
5
6
7
8
9
Input: root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
Output: [1,2,4,7,8,9,10,6,3]
Explanation:
- The left boundary follows the path starting from the root's left child 2 -> 4.
  4 is a leaf, so the left boundary is [2].
- The right boundary follows the path starting from the root's right child 3 -> 6 -> 10.
  10 is a leaf, so the right boundary is [3,6], and in reverse order is [6,3].
- The leaves from left to right are [4,7,8,9,10].
Concatenating everything results in [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3].

Solution:

The result is asking for three part

  1. node on left path
  2. leaves
  3. node in right path

Since we care about ordering.

For nodes on left path, we want to find a node have value and it is not a leave(have child).

For leaves, we want to start from left side, and find a node does not have child. Then search for right leaves.

For nodes on right path, we want to find find a node have value and it is not a leave(have child). But we want to start from right bottom part. that’s why we use post-order traversal.

pre-order for left boundary , in-order for bottom boundary (because it’s basically sea-sawing the bottom) and post-order (but going right node first) for right boundary

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def boundaryOfBinaryTree(self, root: TreeNode) -> List[int]:
        def dfs_leftmost(node):
            if not node or not node.left and not node.right:
                return
            boundary.append(node.val)
            if node.left:
                dfs_leftmost(node.left)
            else:
                dfs_leftmost(node.right)

        def dfs_leaves(node):
            if not node:
                return
            dfs_leaves(node.left)
            if node != root and not node.left and not node.right:
                boundary.append(node.val)
            dfs_leaves(node.right)

        def dfs_rightmost(node):
            if not node or not node.left and not node.right:
                return
            if node.right:
                dfs_rightmost(node.right)
            else:
                dfs_rightmost(node.left)
            boundary.append(node.val)

        if not root:
            return []
        boundary = [root.val]
        dfs_leftmost(root.left)
        dfs_leaves(root)
        dfs_rightmost(root.right)
        return boundary

time complexity: $O(n)$
space complexity: $O(1)$
reference:
related problem: