Problem description:

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

  1. Search for a node to remove.
  2. If the node is found, delete the node.

Follow up: Can you solve it with time complexity O(height of tree)?

Example 1:

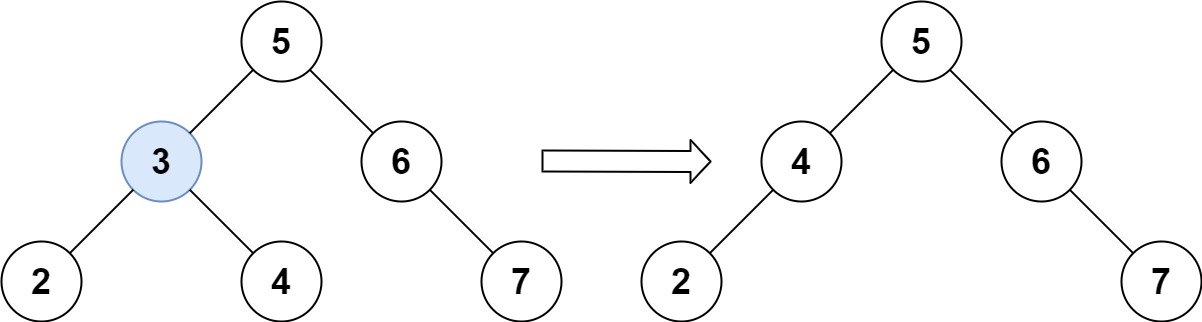
https://assets.leetcode.com/uploads/2020/09/04/del_node_1.jpg

1
2
3
4
5
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

https://assets.leetcode.com/uploads/2020/09/04/del_node_supp.jpg

Example 2:

1
2
3
Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

1
2
Input: root = [], key = 0
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • 105 <= Node.val <= 105
  • Each node has a unique value.
  • root is a valid binary search tree.
  • 105 <= key <= 105

Solution:

Use the BST characteristic

  • if key < root.val: key on left side
  • if key > root.val: key on right side
  • if not both cases, key == root.val

When we find the node we want to delete, we want to find a node to replace root but with minimum reordering. We could use largest node in left subtree OR smallest node in right subtree.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:  
        if not root:
            return
        
        # we always want to delete the node when it is the root of a subtree,
        # so we handle left or right according to the val.
        # if the node does not exist, we will hit the very first if statement and return None.
        if key > root.val:
            root.right = self.deleteNode(root.right, key)
            
        elif key < root.val:
            root.left = self.deleteNode(root.left, key)
        
        # now the key is the root of a subtree
        else:
            # if the subtree does not have a left child, we just return its right child
            # to its father, and they will be connected on the higher level recursion.
            if not root.left:
                return root.right
            
            # if it has a left child, we want to find the max val on the left subtree to 
            # replace the node we want to delete.
            else:
                # try to find the max value on the left subtree
                tmp = root.left
                while tmp.right:
                    tmp = tmp.right
                    
                # replace
                root.val = tmp.val
                
                # since we have replaced the node we want to delete with the tmp, now we don't
                # want to keep the tmp on this tree, so we just use our function to delete it.
                # pass the val of tmp to the left subtree and repeat the whole approach.
                root.left = self.deleteNode(root.left, tmp.val)
        
        return root

time complexity: $O(logn)$
space complexity: $O(1)$
reference:
related problem: