Problem description:

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

Example 1:

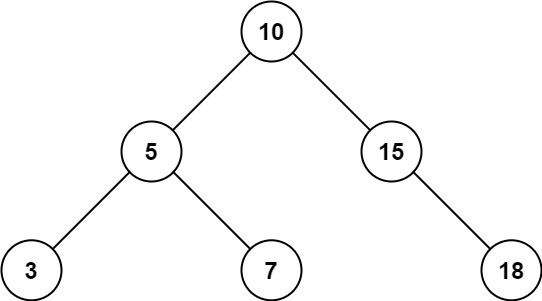
https://assets.leetcode.com/uploads/2020/11/05/bst1.jpg

1
2
3
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

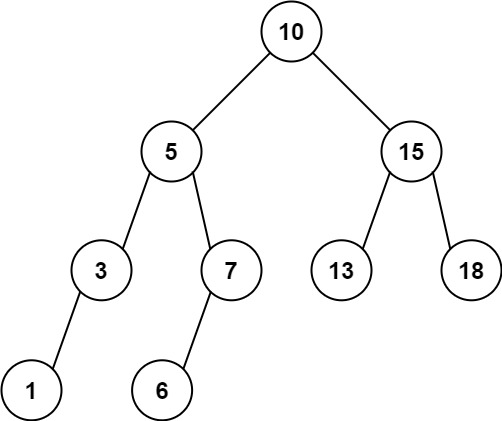
https://assets.leetcode.com/uploads/2020/11/05/bst2.jpg

1
2
3
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints:

  • The number of nodes in the tree is in the range [1, 2 * 104].
  • 1 <= Node.val <= 105
  • 1 <= low <= high <= 105
  • All Node.val are unique.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        # if low <= root val <= high, add to res
        if not root:
            return 0
        if low <= root.val <= high:
            return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)
        elif root.val > high:
            return self.rangeSumBST(root.left, low, high)
        elif root.val < low:
            return self.rangeSumBST(root.right, low, high)

time complexity: $O(n)$
space complexity: $O(1)$, $O(h)$ if count in hidden call stack
reference:
related problem: