Problem description:

Given two numbers, hour and minutes. Return the smaller angle (in degrees) formed between the hour and the minute hand.

Example 1:

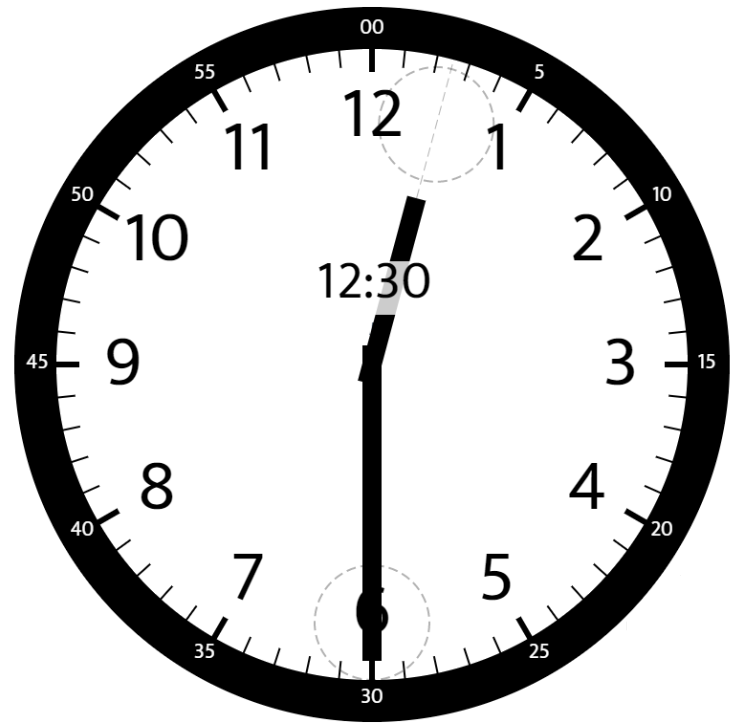
https://assets.leetcode.com/uploads/2019/12/26/sample_1_1673.png

1
2
Input: hour = 12, minutes = 30
Output: 165

Example 2:

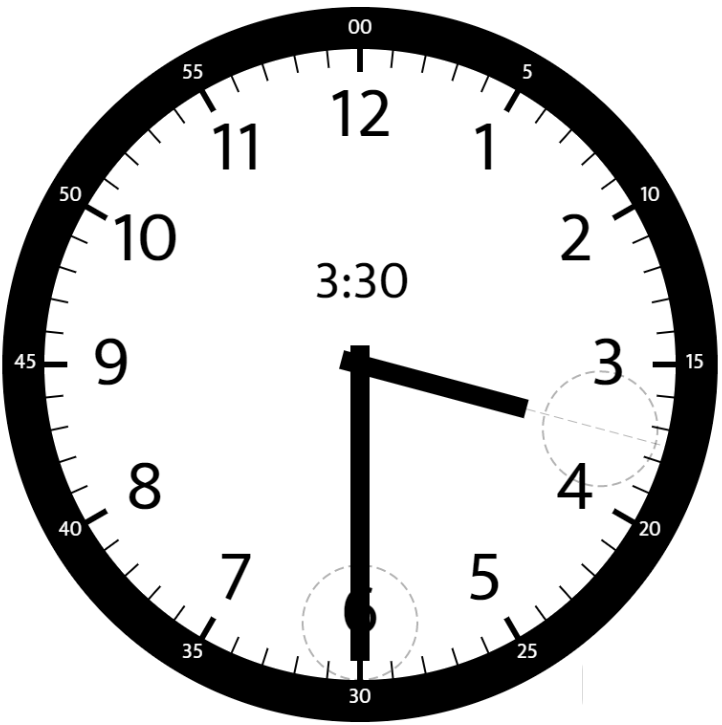
https://assets.leetcode.com/uploads/2019/12/26/sample_2_1673.png

1
2
Input: hour = 3, minutes = 30
Output: 75

Example 3:

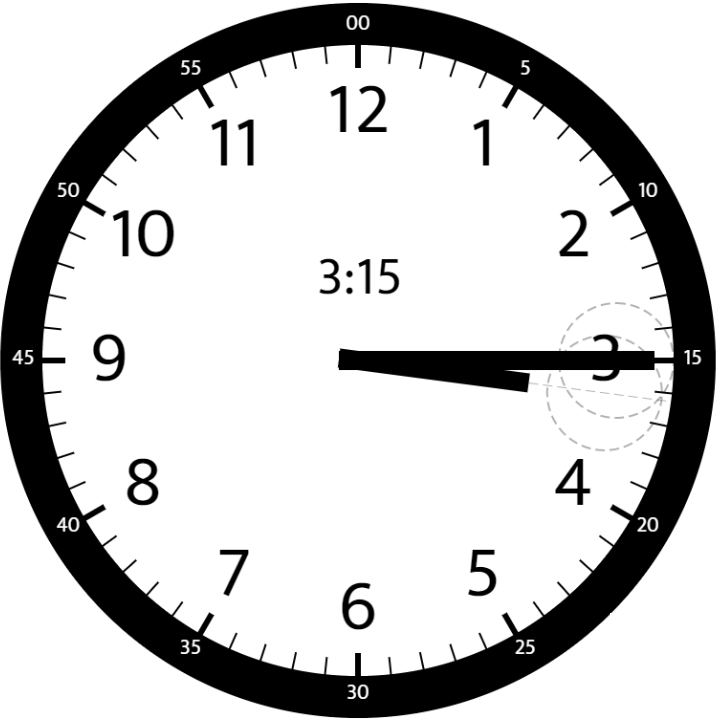
https://assets.leetcode.com/uploads/2019/12/26/sample_3_1673.png

1
2
Input: hour = 3, minutes = 15
Output: 7.5

Example 4:

1
2
Input: hour = 4, minutes = 50
Output: 155

Example 5:

1
2
Input: hour = 12, minutes = 0
Output: 0

Constraints:

  • 1 <= hour <= 12
  • 0 <= minutes <= 59
  • Answers within 10^-5 of the actual value will be accepted as correct.

Solution:

Hour HandIn 12 hours Hour hand complete whole circle and cover 360°So, 1 hour = 360° / 12 = 30°

Since 1 hours = 30°In 1 minute, hours hand rotate -> 30° / 60 = 0.5°So total angle because of minutes by hour hand is minutes/60 * 30 or minutes * 0.5

Minute HandIn 60 minutes Minute Hand completes whole circle and cover 360°.So, 1 minute -> 360° / 60 = 6°

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def angleClock(self, hour: int, minutes: int) -> float:
        # Degree covered by hour hand (hour area + minutes area)
        h = (hour%12 * 30) + (minutes/60 * 30)
        
        # Degree covered by minute hand (Each minute = 6 degree)
        m = minutes * 6
        
        # Absolute angle between them
        angle = abs(m - h)
        
        # If the angle is obtuse (>180), convert it to acute (0<=x<=180)
        if angle > 180:
            angle = 360.0 - angle
        
        return (angle)

time complexity: $O(1)$
space complexity: $O(1)$
reference:
related problem: