Problem description:

You are given an m x n grid grid of values 0, 1, or 2, where:

  • each 0 marks an empty land that you can pass by freely,
  • each 1 marks a building that you cannot pass through, and
  • each 2 marks an obstacle that you cannot pass through.

You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. You can only move up, down, left, and right.

Return the shortest travel distance for such a house. If it is not possible to build such a house according to the above rules, return -1.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

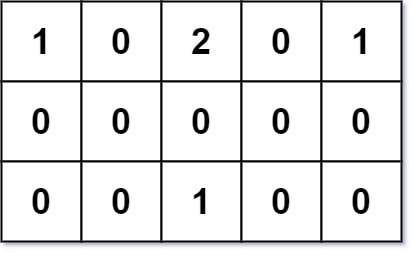
https://assets.leetcode.com/uploads/2021/03/14/buildings-grid.jpg

1
2
3
4
5
Input: grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 7
Explanation: Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2).
The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal.
So return 7.

Example 2:

1
2
Input: grid = [[1,0]]
Output: 1

Example 3:

1
2
Input: grid = [[1]]
Output: -1

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • grid[i][j] is either 0, 1, or 2.
  • There will be at least one building in the grid.

Solution:

  1. need to store each empty slot’s total shortest distance to every building
    use a 2d array to store, shortDist
  2. need to know if an empty slot could reach every building
    use a 2d array to store, hit

For every building[k], do BFS to search every reachable neighbor

  • If neighbor is empty slot update shortDist[i][j] from building[k] to this empty slot (i,j), update hit[i][j] to note this empty slot is reachable by this building
  • If neighbor is a building, increase the count by 1. Because we need to know if building[k] is able to reach every other buildings.
  • use visited array to note the neighbor we visited.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution:
    def shortestDistance(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        buildings = sum(val for line in grid for val in line if val == 1)
        shortDist, hit = [[0]*n for _ in range(m)], [[0]*n for _ in range(m)]
        
        def BFS(startX, startY):
            # walk thourgh all neighbor slots
            # in the meantime, should be able to reach other buildings
            queue = deque([(startX, startY, 0)]) # (x, y, distance)
            count = 1
            visited = [[False]*n for _ in range(m)]
            visited[startX][startY] = True
            while queue:
                x, y, dist = queue.popleft()
                for i, j in ((x+1, y), (x-1, y), (x, y+1), (x, y-1)):
                    if 0 <= i < m and 0 <= j < n and not visited[i][j]:
                        visited[i][j] = True
                        if grid[i][j] == 0:
                            shortDist[i][j] += dist+1
                            hit[i][j] += 1
                            queue.append((i, j, dist+1))
                        elif grid[i][j] == 1:
                            count += 1
            return count == buildings
        
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    if not BFS(i,j):
                        return -1
        
        
        res = float("inf")
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 0 and hit[i][j] == buildings:
                    res = min(res, shortDist[i][j])
        
        return res if res != float("inf") else -1

time complexity: $O(m^2 n^2)$, we need to find number of 1 takes $O(mn)$, in that loop, need to find number of 0 as well takes another $O(mn)$, so $O(m^2 n^2)$
space complexity: $O(m*n)$
reference:
related problem: