Problem description:

You need to construct a binary tree from a string consisting of parenthesis and integers.

The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root’s value and a pair of parenthesis contains a child binary tree with the same structure.

You always start to construct the left child node of the parent first if it exists.

Example 1:

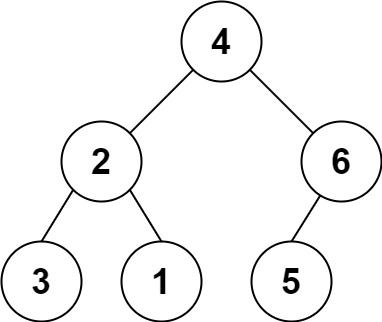
https://assets.leetcode.com/uploads/2020/09/02/butree.jpg

1
2
Input: s = "4(2(3)(1))(6(5))"
Output: [4,2,6,3,1,5]

Example 2:

1
2
Input: s = "4(2(3)(1))(6(5)(7))"
Output: [4,2,6,3,1,5,7]

Example 3:

1
2
Input: s = "-4(2(3)(1))(6(5)(7))"
Output: [-4,2,6,3,1,5,7]

Constraints:

  • 0 <= s.length <= 3 * 104
  • s consists of digits, '(', ')', and '-' only.

Solution:

DFS

have a dfs function to walk through the string
dfs(s, i), take string and start index
build node then recursive calls to build node.left and node.right
return node and index

returning index because we do preorder traversal need next index to build node.right

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def str2tree(self, s: str) -> Optional[TreeNode]:
        '''
        have a dfs function to walk through the string
        dfs(s, i), take string and start index
        build node then recursive calls to build node.left and node.right
        return node and index
        
        returning index because we do preorder traversal
        need next index to build node.right
        '''
        if not s or len(s) == 0:
            return None
        
        root, idx = self.dfs(s, 0)
        return root
        
    def dfs(self, s, i):
        start = i
        if s[start] == '-':
            i += 1
        while i < len(s) and s[i].isdigit():
            i += 1
        node = TreeNode(int(s[start:i]))
        
        if i < len(s) and s[i] == '(': 
            i += 1
            node.left, i = self.dfs(s, i)
            i += 1
        
        if i < len(s) and s[i] == '(':
            i += 1
            node.right, i = self.dfs(s, i)
            i += 1
        
        return node, i

time complexity: $O()$
space complexity: $O()$
reference:
related problem: