Problem description:

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.

A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.

Example 1:

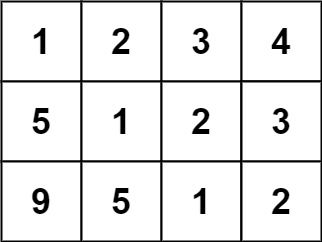
https://assets.leetcode.com/uploads/2020/11/04/ex1.jpg

1
2
3
4
5
6
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.

Example 2:

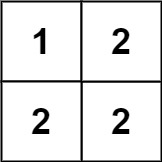
https://assets.leetcode.com/uploads/2020/11/04/ex2.jpg

1
2
3
4
Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal "[1, 2]" has different elements.

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 20
  • 0 <= matrix[i][j] <= 99

Follow up:

  • What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?

  • What if the matrix is so large that you can only load up a partial row into the memory at once?

Solution:

1
2
3
4
5
6
def isToeplitzMatrix(self, m):
        for i in range(len(m) - 1):
            for j in range(len(m[0]) - 1):
                if m[i][j] != m[i + 1][j + 1]:
                    return False
        return True
  • Follow up 1 :

For the follow-up 1, we are only able to load one row at one time, so we have to use a buffer (1D data structure) to store the row info. When next row comes as a streaming flow, we can compare each value (say, matrix[i][j], i>=1, j>=1) to the “upper-left” value in the buffer (buffer[j - 1]); meanwhile, we update the buffer by inserting the 1st element of the current row (matrix[i][0]) to buffer at position 0 (buffer[0]), and removing the last element in the buffer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return true;
        int row = matrix.length;
        int col = matrix[0].length;
        List<Integer> buffer = new LinkedList<>();
        for(int j = 0; j < col; j++) buffer.add(matrix[0][j]);
        for(int i = 1; i < row; i++){
            for(int j = 1; j < col; j++){
                if(buffer.get(j - 1) != matrix[i][j]) return false;
            }
            buffer.remove(buffer.size() - 1);
            buffer.add(0, matrix[i][0]);
        }
        return true;
    }
}
  • Follow up 2: can only load a partial row at one time

two file pointer, the first one start at [0][0], the second one starts at [1][1], load two elements each time, compare and move

Another idea:

We could split the whole matrix vertically into several sub-matrices, while each sub-matrix should have one column overlapped. We repeat the same method in follow-up 1 for each sub-matrix.

For example:

1
2
3
4
5
[1 2 3 4 5 6 7]              [1 2 3 4]              [4 5 6 7]
[0 1 2 3 4 5 6]              [0 1 2 3]              [3 4 5 6]
[1 0 1 2 3 4 5]     -->      [1 0 1 2]       +      [2 3 4 5]
[2 1 0 1 2 3 4]              [2 1 0 1]              [1 2 3 4]
[3 2 1 0 1 2 3]              [3 2 1 0]              [0 1 2 3]

time complexity: $O()$
space complexity: $O()$
reference:
related problem: