Problem description:

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

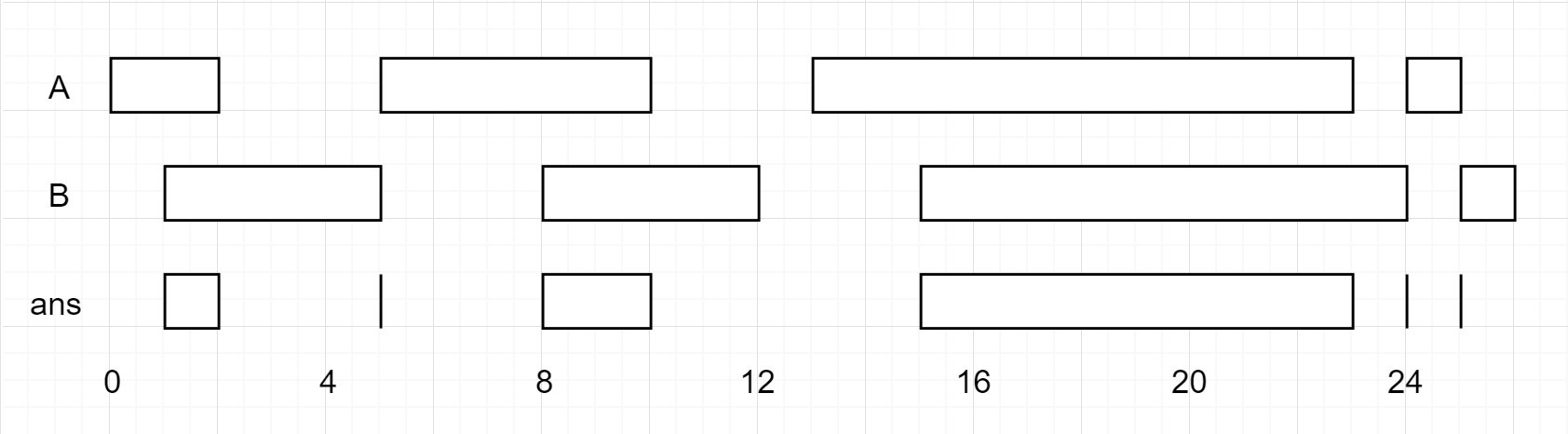
https://assets.leetcode.com/uploads/2019/01/30/interval1.png

1
2
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Solution:

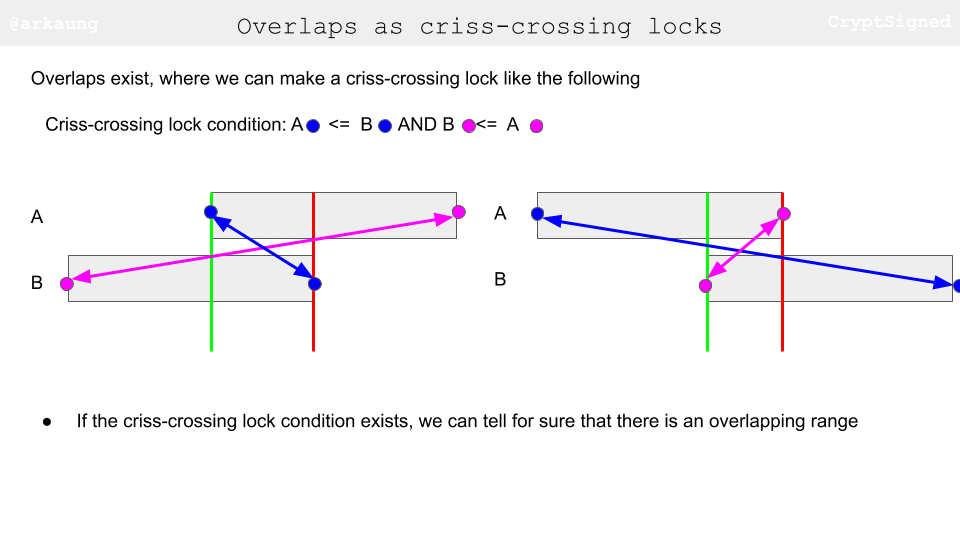
  1. Detect overlap and append to res

https://assets.leetcode.com/users/arkaung/image_1590249888.png

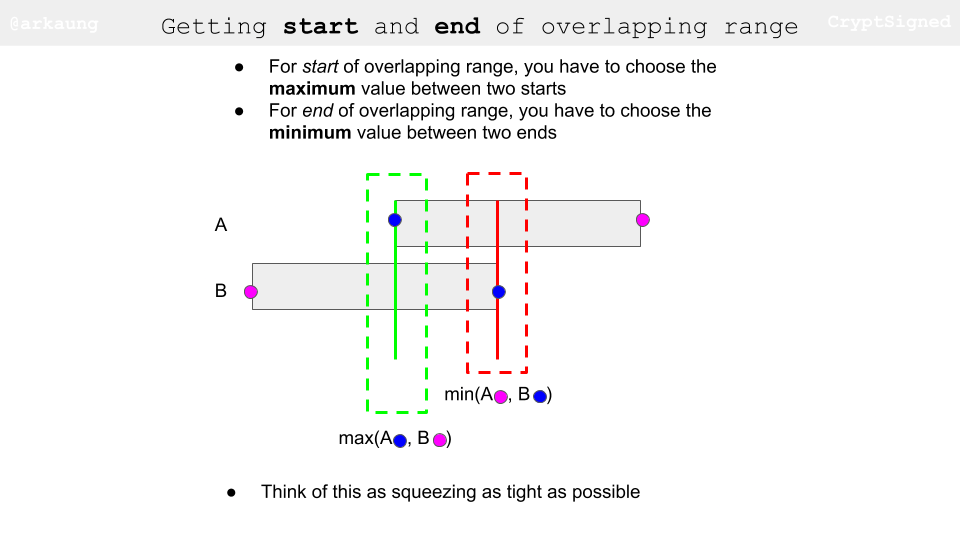
https://assets.leetcode.com/users/arkaung/image_1590249893.png

  1. Incrementing pointers

Move the one that has the smaller end

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def intervalIntersection(self, A: List[List[int]], B: List[List[int]]) -> List[List[int]]:
        i = 0
        j = 0   
        result = []
        while i < len(A) and j < len(B):
            a_start, a_end = A[i]
            b_start, b_end = B[j]
            if a_start <= b_end and b_start <= a_end:
								# Criss-cross lock
                result.append([max(a_start, b_start), min(a_end, b_end)])   
            if a_end <= b_end:       # Exhausted this range in A
                i += 1               # Point to next range in A
            else:                    # Exhausted this range in B
                j += 1               # Point to next range in B
        return result

time complexity: $O()$
space complexity: $O()$
reference:
related problem: