Problem description:

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is tree consisting of that node, plus the set of all descendants of that node.

Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

Example 1:

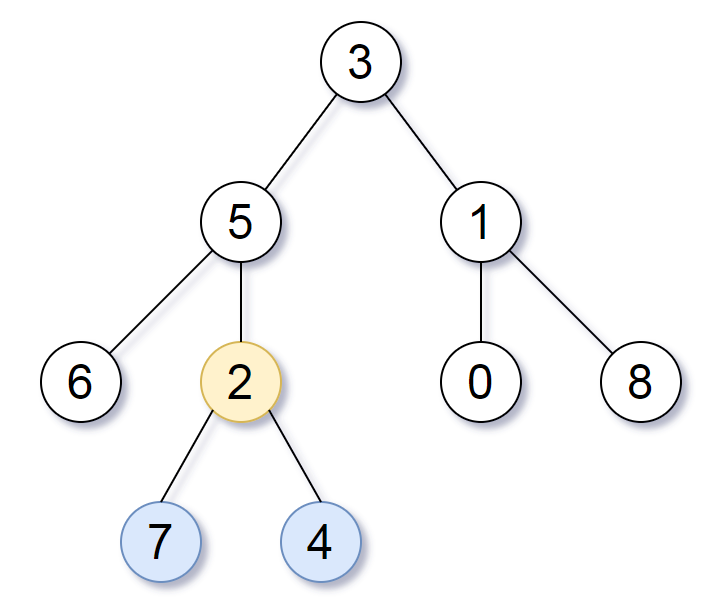
https://s3-lc-upload.s3.amazonaws.com/uploads/2018/07/01/sketch1.png

1
2
3
4
5
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

1
2
3
Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

1
2
3
Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

Constraints:

  • The number of nodes in the tree will be in the range [1, 500].
  • 0 <= Node.val <= 500
  • The values of the nodes in the tree are unique.

Solution:

D934EEB5-E953-4154-9743-BB0F1DA97872.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode: 
        def dfs(root):
            if not root:
                return 0, None
            l, r = dfs(root.left), dfs(root.right)
            if l[0] > r[0]:
                return l[0]+1, l[1]
            elif l[0] < r[0]:
                return r[0]+1, r[1]
            else:
                return l[0]+1, root
        return dfs(root)[1]

time complexity: $O()$
space complexity: $O()$
reference:
related problem: