Problem description:

In a given 2D binary array grid, there are two islands. (An island is a 4-directionally connected group of 1s not connected to any other 1s.)

Now, we may change 0s to 1s so as to connect the two islands together to form 1 island.

Return the smallest number of 0s that must be flipped. (It is guaranteed that the answer is at least 1.)

Example 1:

1
2
Input: grid = [[0,1],[1,0]]
Output: 1

Example 2:

1
2
Input: grid = [[0,1,0],[0,0,0],[0,0,1]]
Output: 2

Example 3:

1
2
Input: grid = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
Output: 1

Constraints:

  • 2 <= grid.length == grid[0].length <= 100
  • grid[i][j] == 0 or grid[i][j] == 1

Solution:

We first paint one of the islands using DFS with color 2, so we can easily identify island #1 and island #2.

Then we start expanding island #2 by paining connected empty area. Each round, we increase the color (3, 4, and so on) so we can keep track of the newly painted area. This ends when we “bump” into the first island.

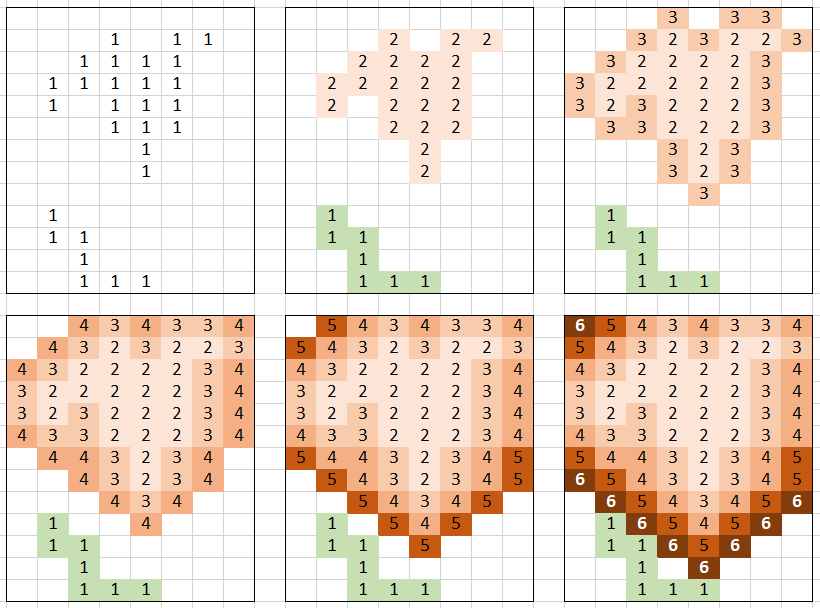
https://assets.leetcode.com/users/votrubac/image_1541488072.png

The fact that we are increasing the color is also useful for the backtracking, if we need to return the coordinates of the bridge.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def shortestBridge(self, grid: List[List[int]]) -> int:
        '''
        paint the island
        
        '''
        def paint(i, j):
            if i < 0 or j < 0 or i >= m or j >= n or grid[i][j] != 1:
                return 0
            grid[i][j] = 2
            return 1+ paint(i+1, j) + paint(i-1, j) + paint(i, j+1) + paint(i, j-1)
        
        def expand(i, j, color):
            if i < 0 or j < 0 or i >= m or j >= n: return False
            if grid[i][j] == 0:
                grid[i][j] = color + 1
            return grid[i][j] == 1
            
            
        print(grid)
        found = False
        m, n = len(grid), len(grid[0])
        for i in range(m):
            if found: break
            for j in range(n):
                if found: break
                if grid[i][j] == 1:
                    found = paint(i,j)
        
        color = 2
        while True:
            for i in range(m):
                for j in range(n):
                    if grid[i][j] == color and (expand(i-1, j, color) or expand(i+1, j, color) or expand(i, j+1, color) or expand(i, j-1, color)):
                        return color-2
            color += 1

time complexity: $O()$
space complexity: $O()$
reference:
related problem: