Problem description:

Given a root of an N-ary tree, you need to compute the length of the diameter of the tree.

The diameter of an N-ary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root.

(Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value.)

Example 1:

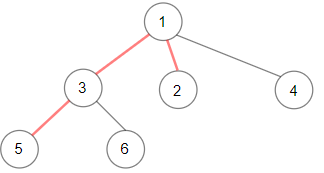
https://assets.leetcode.com/uploads/2020/07/19/sample_2_1897.png

1
2
3
Input: root = [1,null,3,2,4,null,5,6]
Output: 3
Explanation:Diameter is shown in red color.

Example 2:

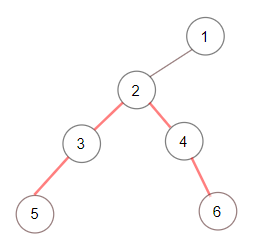
https://assets.leetcode.com/uploads/2020/07/19/sample_1_1897.png

1
2
Input: root = [1,null,2,null,3,4,null,5,null,6]
Output: 4

Example 3:

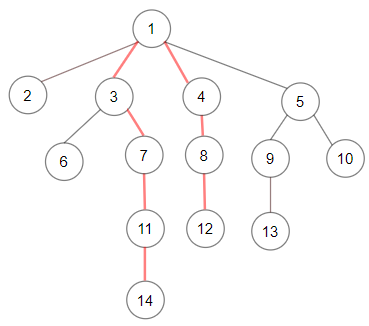
https://assets.leetcode.com/uploads/2020/07/19/sample_3_1897.png

1
2
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 7

Constraints:

  • The depth of the n-ary tree is less than or equal to 1000.
  • The total number of nodes is between [1, 104].

Solution:

Need to have two variable first and second to record the top 2 longest path under current root.

Have a global variable res to keep result

Only need to return the longest path to parent, which is first+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children if children is not None else []
"""

class Solution:
    def diameter(self, root: 'Node') -> int:
        self.res = 0
        self.dfs(root)
        return self.res
    
    def dfs(self, root):
        if not root: return 0
        first, second = 0, 0
        for i in range(len(root.children)):
            depth = self.dfs(root.children[i])
            if depth > first:
                first, second = depth, first
            elif depth > second:
                second = depth
            self.res = max(self.res, first+second)
        return first+1

time complexity: $O()$
space complexity: $O()$
reference:
related problem: